60.1K

Verified Solution

Link Copied!

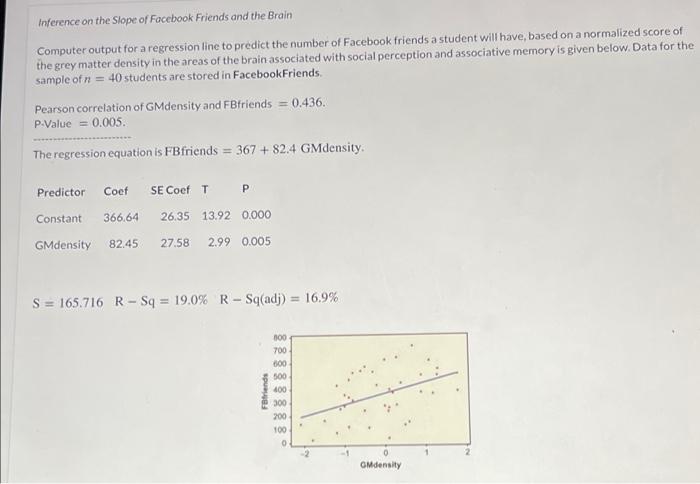
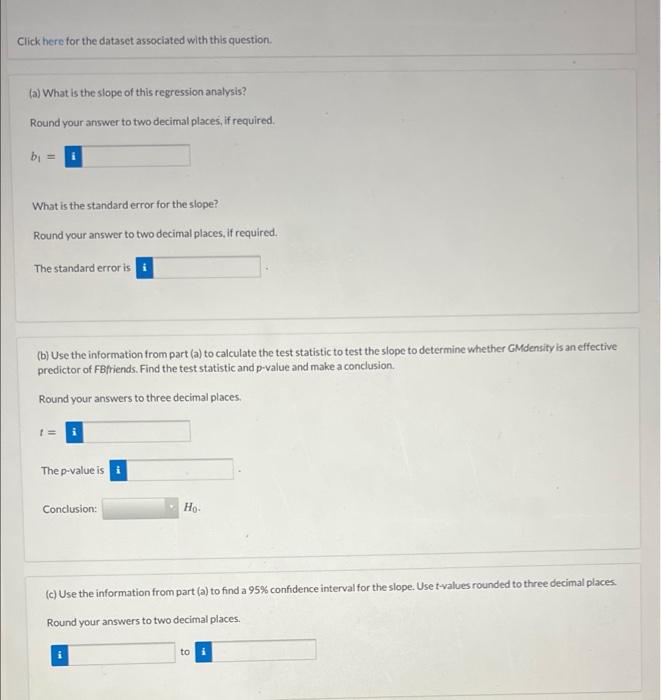Inference on the slope of Facebook Friends and the Brain Computer output for a regression line to predict the number of Facebook friends a student will have, based on a normalized score of the grey matter density in the areas of the brain associated with social perception and associative memory is given below. Data for the sample of n = 40 students are stored in FacebookFriends Pearson correlation of GMdensity and FBfriends = 0.436. P.Value = 0.005 The regression equation is FBfriends = 367 + 82.4 GMdensity Predictor Coef SE Coef T P Constant 366.64 26,35 13.92 0.000 GMdensity 82.45 27.58 2.99 0.005 S = 165.716 R-Sq = 19.0% R - S (adj) = 16.9% Friends 100 700 000 500 400 300 200 100 0 GMdensity Click here for the dataset associated with this question (a) What is the slope of this regression analysis? Round your answer to two decimal places, if required bi = What is the standard error for the slope? Round your answer to two decimal places, if required. The standard error is (b) Use the information from part (a) to calculate the test statistic to test the slope to determine whether GMdensity is an effective predictor of FBfriends. Find the test statistic and p-value and make a conclusion Round your answers to three decimal places, = i The p-value is i Conclusion: HO (c) Use the information from part (a) to find a 95% confidence interval for the slope. Use t-values rounded to three decimal places. Round your answers to two decimal places. to

Answer & Explanation Solved by verified expert

See Answer