60.1K
Verified Solution
 Link Copied!
Link Copied!
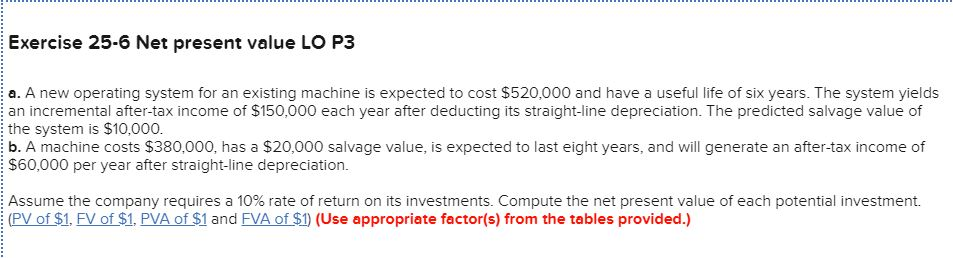
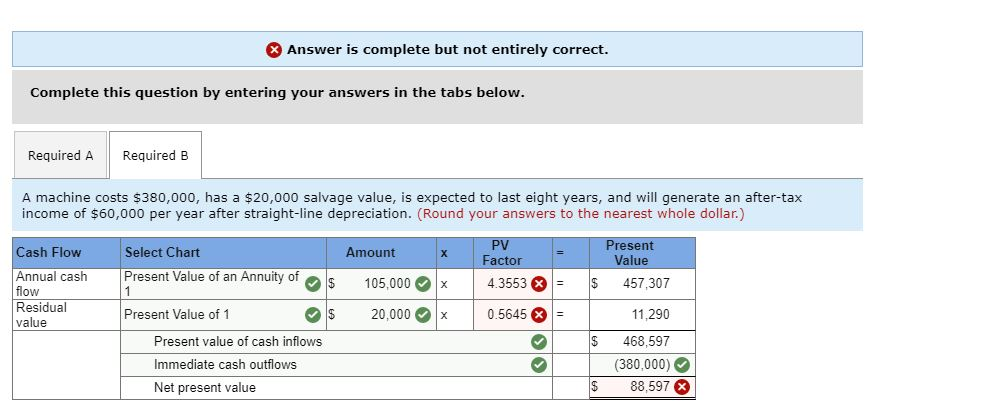
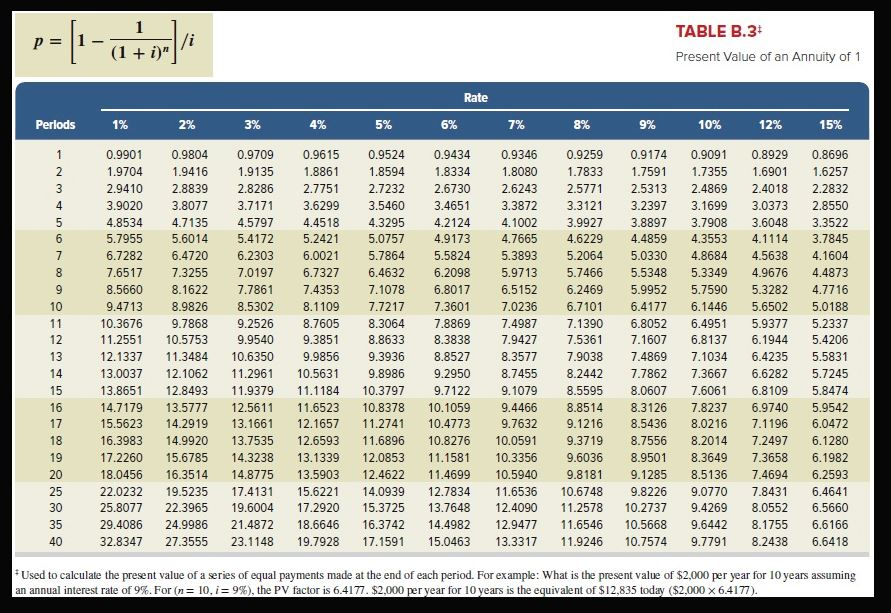
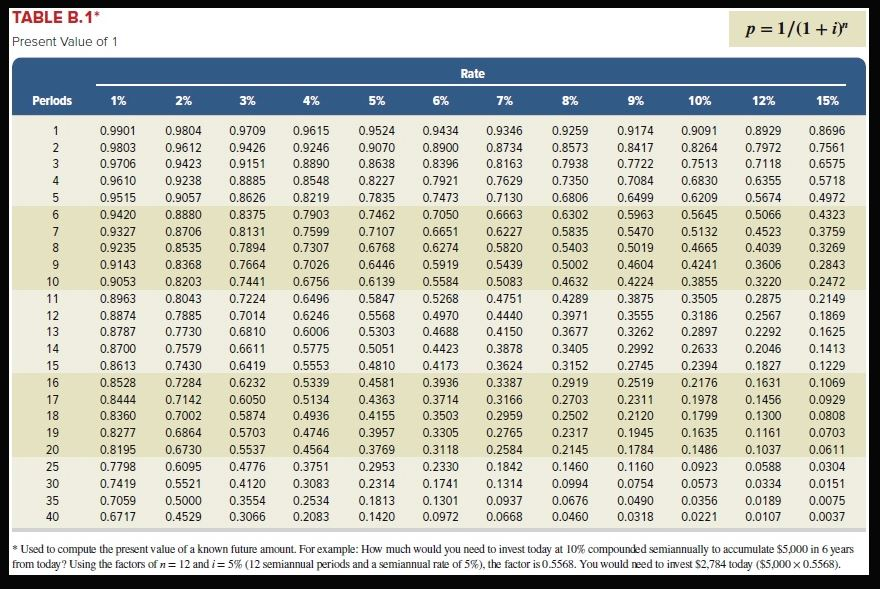
Exercise 25-6 Net present value LO P3 a. A new operating system for an existing machine is expected to cost $520,000 and have a useful life of six years. The system yields an incremental after-tax income of $150,000 each year after deducting its straight-line depreciation. The predicted salvage value of the system is $10,000. b. A machine costs $380,000, has a $20,000 salvage value, is expected to last eight years, and will generate an after-tax income of $60,000 per year after straight-line depreciation. Assume the company requires a 10% rate of return on its investments. Compute the net present value of each potential investment. (PV of $1. FV of $1. PVA of $1 and FVA of $1) (Use appropriate factor(s) from the tables provided.) X Answer is complete but not entirely correct. Complete this question by entering your answers in the tabs below Required A Required B A machine costs $380,000, has a $20,000 salvage value, is expected to last eight years, and will generate an after-tax income of $60,000 per year after straight-line depreciation. (Round your answers to the nearest whole dollar.) PV Present Value Cash Flow Select Chart Amount X Factor Present Value of an Annuity of Annual cash flow Residual s 4.3553( 105,000 S 457,307 1 20,000 x Present Value of 1 0.5645 11,290 value Present value of cash inflows 468,597 Immediate cash outflows (380,000) 88,597 x Net present value 1 TABLE B.3 /i (1i)" Present Value of an Annuity of 1 Rate Perlods 1% 2% 3% 4% 5% 6% 7% 8% 9% 10% 12% 15% 0.9524 0.9346 0.9901 0.9804 0.9709 0.9615 0.9434 0.9259 0.9174 0.9091 0.8929 0.8696 1.8080 1.7833 2 1.9704 1.9416 1.9135 1.8861 1.8594 1.8334 1.7591 1.7355 1,6901 1.6257 3 2.9410 2.8839 2.8286 2.7751 2,7232 2.6730 2.6243 2.5771 2.5313 2.4869 2.4018 2.2832 3.0373 4 3.9020 3.8077 3.7171 3.6299 3.5460 3.4651 3.3872 3.3121 3.2397 3.1699 2.8550 4,8534 4.4518 4.2124 4.1002 3.8897 3.7908 5 4.7135 4.5797 4.3295 3.9927 3.6048 3.3522 5.7955 4,7665 6 5.6014 5.4172 5.2421 5.0757 4.9173 4.6229 4.4859 4.3553 4.1114 3.7845 7 5.3893 4.8684 6.7282 6.4720 6.2303 6.0021 5.7864 5,5824 5.2064 5.0330 4,5638 4.1604 7.6517 4.9676 7.3255 7.0197 6,7327 6.4632 6.2098 5.9713 5.7466 5.5348 5.3349 4.4873 4,7716 8.5660 8.1622 7.7861 7.4353 7.1078 6.8017 6.5152 6.2469 5.9952 5.7590 5.3282 8.5302 6,7101 10 9.4713 8.9826 8.1109 7.7217 7.3601 7.0236 6.4177 6.1446 5.6502 5.0188 9.2526 7,4987 11 10.3676 9.7868 8.7605 8.3064 7.8869 7.1390 6.8052 6.4951 5.9377 5.2337 10.5753 6.8137 12 11.2551 9.9540 9.3851 8.8633 8.3838 7.9427 7.5361 7.1607 6.1944 5.4206 7.9038 13 12.1337 11.3484 10.6350 9.9856 9.3936 8.8527 8.3577 7.4869 7.1034 6.4235 5.5831 10.563 13.0037 9.2950 6.6282 14 12.1062 11.296 9.8986 8.7455 8.2442 7.7862 7.3667 5.7245 8.0607 15 13.8651 12.8493 11.9379 11.1184 10.3797 9.7122 9.1079 8.5595 7.6061 6.8109 5.8474 11.6523 10.8378 16 14.7179 13.5777 12.5611 10.1059 9.4466 8.8514 8.3126 7.8237 6.9740 5.9542 12.1657 8.0216 6,0472 17 15.5623 14.2919 13.1661 11.2741 10.4773 9.7632 9.1216 8.5436 7.1196 8.2014 18 16.3983 14.9920 13.7535 12.6593 11.6896 10.8276 10.0591 9.3719 8.7556 7.2497 6.1280 19 9.6036 8.3649 7.3658 17.2260 15.6785 14.3238 13.1339 12.0853 11.1581 10.3356 8.9501 6.1982 18.0456 16.3514 11.4699 20 14.8775 13.5903 12.4622 10.5940 9.8181 9.1285 8.5136 7.4694 6.2593 25 15.6221 14.0939 10.6748 22.0232 19.5235 17.413 12.7834 11.6536 9.8226 9.0770 7,8431 6.4641 30 8.0552 25.8077 22.3965 19.6004 17.2920 15.3725 13.7648 12.4090 11.2578 10.2737 9.4269 6.5660 29.4086 18.6646 8.1755 35 24.9986 21.4872 16.3742 14.4982 12.9477 11.6546 10.5668 9.6442 6.6166 6.6418 40 32.8347 27.3555 23.1148 19.7928 17.1591 15.0463 13.3317 11.9246 10.7574 9,7791 8.2438 Used to calculate the present value of a series of equal payments made at the end of each period. For example: What is the present value of $2,000 per year for 10 years assuming an annual interest rate of 9%. For (n = 10, i= 9 % ) , the PV factor is 6.4177. $2,000 per year for 10 years is the equivalent of $12,835 today ($2,000 x 6.4177) TABLE B.1* p 1/(1i Present Value of 1 Rate Perlods 1% 2% 3% 4% 5% 6% 7% 8% 9% 10% 12% 15% 0.9901 0.9615 0.9259 1 0.9804 0.9709 0.9524 0.9434 0.9346 0.9174 0.9091 0.8929 0.8696 0.8900 0.8264 2 0.9803 0.9612 0.9426 0.9246 0.9070 0.8734 0.8573 0.8417 0.7972 0.7561 0.9151 0.8396 0.6575 0.9706 0.9423 0.8890 0.8638 0.8163 0.7938 0.7722 0.7513 0.7118 4 0.9610 0.9238 0.8885 0.8548 0.8227 0.7921 0.7629 0.7350 0.7084 0.6830 0.6355 0.5718 5 0.9515 0.9057 0.8626 0.8219 0.7835 0.7473 0.7130 0.6806 0.6499 0.6209 0.5674 0.4972 0.9420 0.6302 0.5066 0.8880 0.8375 0.7903 0.7462 0.7050 0.6663 0.5963 0.5645 0.4323 0.583 0.6651 0.5132 .4523 7 0.9327 0.8706 0.813 0.7599 0.7107 0.6227 0.5470 .3759 8 0.5019 0.9235 0.8535 0.7894 0.7307 0.6768 0.6274 0.5820 0.5403 0.4665 0.4039 0.3269 0.7664 0.2843 0.9143 0.8368 0.7026 0.6446 0.5919 0.5439 0.5002 0.4604 0.4241 0.3606 0.6756 0.6139 0.2472 10 0.9053 0.8203 0.7441 0.5584 0.5083 0.4632 0.4224 0.3855 0.3220 0.5268 0.3505 0.2875 11 0.8963 0.8043 0.7224 0.6496 0.5847 0.4751 0.4289 0.3875 0.2149 12 0.8874 0.7885 0.7014 0.6246 0.5568 0.4970 0.4440 0.3971 0.3555 0.3186 0.2567 0.1869 0.6006 0.4688 13 0.8787 0.7730 0.6810 0.5303 0.4150 0.3677 0.3262 0.2897 0.2292 0.1625 0.8700 0.7579 0.5775 0.2046 14 0.6611 0.5051 0.4423 0.3878 0.3405 0.2992 0.2633 0.1413 0.6419 15 0.8613 0.7430 0.5553 0.4810 0.4173 0.3624 0.3152 0.2745 0.2394 0.1827 0.1229 16 0.8528 0.7284 0.6232 0.5339 0.4581 0.3936 0.3387 0.2919 0.2519 0.2176 0.1631 0.1069 0.7142 0.1978 17 0.8444 0.6050 0.5134 0.4363 0.3714 0.3166 0.2703 0.2311 0.1456 0.0929 0.7002 0.4155 0.2502 0.1799 0,0808 18 0.8360 0.5874 0.4936 0.3503 0.2959 0.2120 0.1300 0.6864 0.0703 19 0.8277 0.5703 0.4746 0.3957 0.3305 0.2765 0.2317 0.1945 0.1635 0.1161 0.6730 0.5537 0.1784 0.1037 0.0611 20 0.8195 0.4564 0.3769 0.3118 0.2584 0.2145 0.1486 25 0.7798 0.6095 0.4776 0.3751 0.2953 0.2330 0.1842 0.1460 0.1160 0.0923 0.0588 0.0304 0.7419 30 0.5521 0.4120 0.3083 0.2314 0.1741 0.1314 0.0994 0.0754 0.0573 0.0334 0.0151 35 0.7059 0.5000 0.0676 0.3554 0.2534 0.1813 0.1301 0.0937 0.0490 0.0356 0.0189 0.0075 40 0.0037 0.6717 0.4529 0.3066 0.2083 0.1420 0.0972 0.0668 0.0460 0.0318 0.0221 0.0107 Used to compute the present value of a known future amount. For example: How much would you need to invest today at 10 % compounded semiannually to accumulate $5,000 in 6 years from today? Using the factors of n= 12 and i- 5 % ( 12 semiannual periods and a semiannual rate of 5%) , the factor is 0.5568. You would need to invest $2,784 today ($5,000 x 0.5568)
Answer & Explanation
Solved by verified expert




