70.2K

Verified Solution

Link Copied!

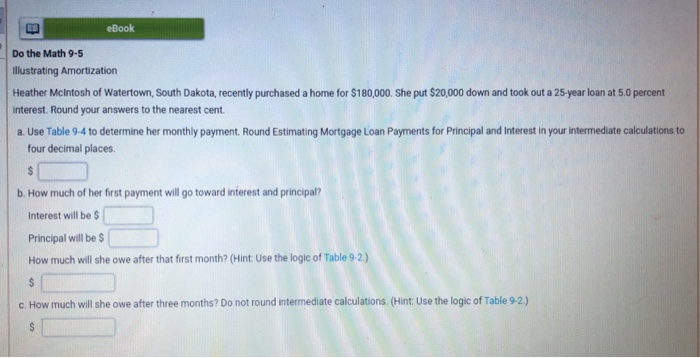
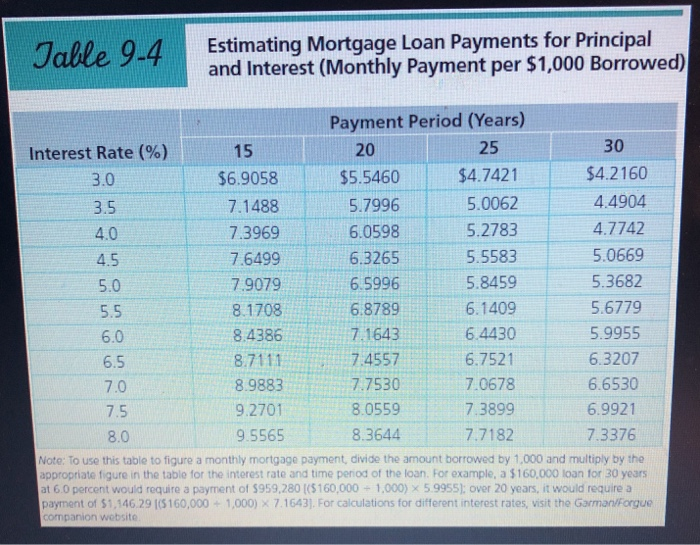
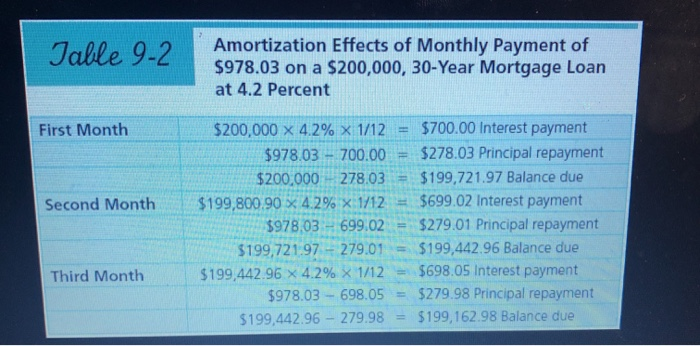eBook Do the Math 9-5 illustrating Amortization Heather McIntosh of Watertown, South Dakota, recently purchased a home for $180,000. She put $20,000 down and took out a 25-year loan at 5.0 percent interest. Round your answers to the nearest cent. a. Use Table 9-4 to determine her monthly payment. Round Estimating Mortgage Loan Payments for Principal and Interest in your intermediate calculations to four decimal places $ b. How much of her first payment will go toward interest and principal? Interest will be $ Principal will be $ How much will she owe after that first month? (Hint Use the logic of Table 9.2.) c. How much will she owe after three months? Do not round intermediate calculations. (Hint: Use the logic of Table 9-2.) Table 9-4 Estimating Mortgage Loan Payments for Principal and Interest (Monthly Payment per $1,000 Borrowed) 3.0 4.0 4.5 Payment Period (Years) Interest Rate (%) 15 20 25 30 $6.9058 $5.5460 $4.7421 $4.2160 3.5 7.1488 5.7996 5.0062 4.4904 7.3969 6.0598 5.2783 4.7742 7.6499 6.3265 5.5583 5.0669 5.0 7.9079 6.5996 5.8459 5.3682 5.5 8.1708 6.8789 6.1409 5.6779 6.0 8.4386 7.1643 6.4430 5.9955 6.5 8.7111 7.4557 6.7521 6.3207 8.9883 7.7530 7.0678 6.6530 7.5 9.2701 8.0559 7.3899 6.9921 9.5565 8.3644 7.7182 7.3376 Note: To use this table to figure a monthly mortgage payment, divide the amount borrowed by 1,000 and multiply by the appropriate figure in the table for the interest rate and time period of the loan. For example, a $160,000 loan for 30 years at 6.0 percent would require a payment of $959,280 (5160,000 - 1,000) X 5.9955): over 20 years, it would require a payment of $1,146.29 (5160,000 + 1,000) X 7.1643). For calculations for different interest rates, visit the Garman/Forgue companion website 7.0 Table 9-2 Amortization Effects of Monthly Payment of $978.03 on a $200,000, 30-Year Mortgage Loan at 4.2 Percent First Month Second Month $978.03 - 700.00 = $278.03 Principal repayment $200,000 278.03 = $199,721.97 Balance due $199,800.90 X 4.2% X:1/12 = $699.02 Interest payment $978.03 - 699.02 = $279.01 Principal repayment $199,72197 - 279.01 = $199,442.96 Balance due $199,442.96 x 4.2% X 1/12 = $698.05 Interest payment $978.03 - 698.05 = $279.98 Principal repayment $199,442.96 - 279.98 = $199,162.98 Balance due Third Month

Answer & Explanation Solved by verified expert

See Answer